Common Formulas

Common Formulas#

Note

This page contains formulas for statistical quantities we’ve discussed so far. We’ll add more as we go along.

# NumPy for basic statistics and linear algebra
import numpy as np

Summarizing single variables#

Mode#

Definition: The most common value in the data

mode = np.mode(data)

Median#

Definition: The middle value after sorting the data from lowest to highest - or the average of middle values if there is an even number of data points

Intuition: A simple summary “model” of the data that minimizes the the sum of absolute errors - i.e. the absolute distance of each data point from the median

median = np.median(data)

Mean#

Definition: The average of all the data points - often called the expected value in other settings

Intuition: A simple summary “model” of the data that minimizes the the sum of squared errors - i.e. the squared distance of each data point from the mean

\[\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i\]
mean = np.mean(data)

Variance#

Definition: The average of the squared distance of each data point from the mean; we use \(n-1\) instead of \(n\) to account for the sample mean \(\bar{x}\) that we depend upon

Intuition v1: How dispersed the data are around the mean
Intuition v2: The average prediction-error of the mean as a model for the data

\[\sigma^2_x = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2\]
variance = np.var(data)

Standard Deviation#

Definition: The square root of the variance

Intuition: Variance in units of standardized distance from the mean

\[\sigma_x = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2}\]
std_dev = np.std(data)

Z-Score#

Definition: The standardized distance of each data point from the mean by subtracting the mean and dividing by standard deviation

Intuition: Centering and scaling the data into units of “standardized distance from the mean” to make data comparable across different measurement scales

\[z_i = \frac{x_i - \bar{x}}{\sigma_x}\]
# Easiest
from scipy.stats import zscore

z_scores = zscore(data)

# Manually
z_scores = (data - np.mean(data)) / np.std(data)

# Or if data is an array you can use method, i.e. "." syntax 
z_scores = (data - data.mean()) / data.std()

Vector Norm#

Definition: Square-root of the sum of each element squared

Intuition: Reflects the magnitude/length of a vector of data, specifically in terms of how far it is from 0 (the origin). If variance is average spread of the data around the mean, the norm is the total spread of the data (distance) from the value 0.

\[\|\mathbf{x}\| = \sqrt{\sum_{i=1}^n x_i^2}\]

Linear algebra style:

\[\|\mathbf{x}\| = \sqrt{\mathbf{x}^\top\mathbf{x}}\]
# Easiest
norm = np.linalg.norm(x)

# Manually:
norm = np.sqrt(np.sum(x**2))

# linear algebra style
norm = np.sqrt(np.dot(x.T, x))

Summarizing relationships#

Dot Product#

Definition: Sum of the products of each pair of elements

Intuition: If x and y “move together” the dot-product will be higher - but sensitive to the units of the measurement

\[\begin{split} \begin{align*} dot(x,y) &= \mathbf{x}^\top\mathbf{y} \\ &= \sum_{i=1}^n x_i y_i \end{align*} \end{split}\]
dot_product = np.dot(x, y)

# Manually
np.sum(x * y)

Cosine Similarity#

Definition: Dot product normalized, i.e. divided by, the product of vector norms

Intuition: Scale the dot-product to standardized units of “distance from 0” - no longer sensitive to the units of the measurement and bounded between -1 and 1

\[\begin{split} \begin{align*} \text{cosine}(x, y) &= \frac{dot(x,y)}{\|\mathbf{x}\|\|\mathbf{y}\|} \\ &= \frac{\mathbf{x}^\top\mathbf{y}}{\sqrt{\mathbf{x}^\top\mathbf{x}} \sqrt{\mathbf{y}^\top\mathbf{y}}} \end{align*}\end{split}\]
# X norm - manually
x_norm = np.sqrt(np.sum(x**2))

# Y norm - easier just use numpy
y_norm = np.linalg.norm(y)

# Scale dot product to standardized units of "*distance from 0*"
cosine_similarity = np.dot(x, y) / (x_norm * y_norm)

# OR
from scipy.spatial.distance import cosine

# Convert distance to similarity using 1-cosine
cosine_similarity = 1 - cosine(x, y)

Average Dot/Inner Product#

Definition: Just divide dot-product by the number of elements

Intuition: Behaves just like the dot-product, but scale is more intuitive to understand - still sensitive to the units of the measurement

\[\begin{split}\begin{align*} average \ dot(x,y) &= \frac{\mathbf{x}^\top\mathbf{y}}{n} \\ &= \frac{1}{n} \sum_{i=1}^n x_i y_i \end{align*} \end{split}\]
avg_dot_product = np.dot(x, y) / len(x)

Covariance#

Definition: Mean-centered average dot-product - use \(n-1\) instead of \(n\) to account for the sample mean(s) we depend upon

Intuition: Measure how much x and y “move together” around their respective means; “anchors” the average dot product to the centers (means) of each variable - still sensitive to the units of measurement

\[\begin{split} \begin{align*} cov(x,y) &= \frac{\mathbf{(x - \bar{x})}^\top\mathbf{(y-\bar{y})}}{n-1} \\ &= \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \end{align*} \end{split}\]
covariance = np.dot(x - x.mean(), y - y.mean()) / (len(x) - 1)

# OR
# Returns 2d array: off-diagonals are covariance; diagonals are variances
covariance = np.cov(x, y)

Pearson Correlation#

Intuition: Measure how much x and y “move together” around their respective means - in units of standardized distance from the mean - i.e. z-scores - best used when you want to detect linear relationships

Definition v1: Covariance normalized by product of standard deviations

\[\begin{split}\begin{align*} corr(x,y) &= \frac{cov(x, y)}{\sigma_x\sigma_y} \\ &= \frac{cov(x,y)}{\sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \bar{y})^2}} \end{align*} \end{split}\]
correlation = covariance / np.std(x) * np.std(y)

Definition v2: Average dot-product of z-scores

\[\begin{split} \begin{align*} r_{x,y} &= \frac{z_x^\top z_y}{n-1} \\ &= \frac{1}{n-1} \sum_{i=1}^n z_{x_i} z_{y_i} \\ &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \end{align*} \end{split}\]
from scipy.stats import zscore

z_x = zscore(x)
z_y = zscore(y)

correlation = np.dot(z_x, z_y) / (len(x) - 1)

Useful functions in practice:

# Scipy
from scipy.stats import pearsonr
result = pearsonr(x, y)

result.statistic # correlation
result.pvalue # p-value
result.confidence_interval # 95% confidence interval

# Numpy
# Off-diagonals are correlation
correlation_matrix = np.corrcoef(x, y)

# Or as single array
2d_xy = np.vstack([x,y])
correlation_matrix = np.corrcoef(2d_xy)

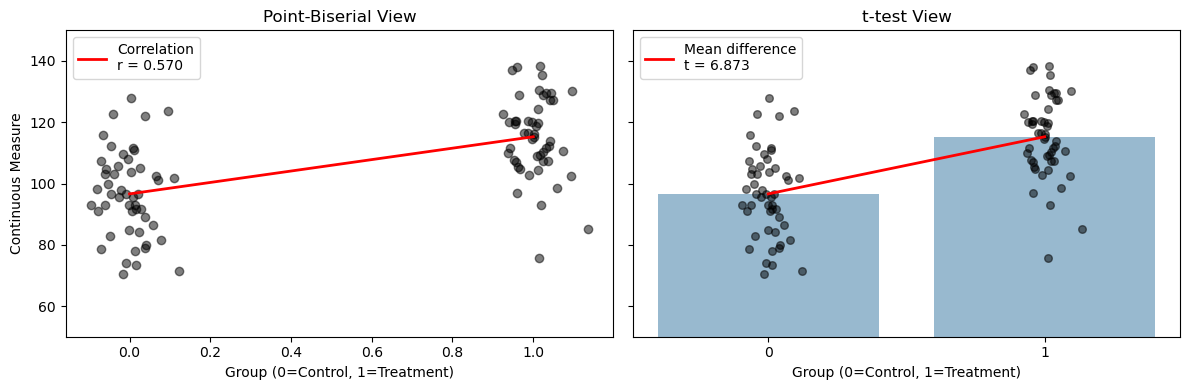
Point-Biserial Correlation (Special Case)#

Definition: Point-biserial correlation is a special case of Pearson’s correlation used when one variable is binary (e.g., 0/1, False/True) and the other is continuous.

Intuition: When one of your variables is binary, the correlation is akin to a test of the difference between two means, i.e. an indepdendent samples t-test.

Figure 1 
from scipy.stats import pointbiserialr

result = pointbiserialr(x_binary, y)

# Equivalent to:
from scipy.stats import pearsonr
result = pearsonr(x_binary, y)

In fact you can convert between the point biserial \(r\) and the student’s \(t\) using the following formulas:

\[\begin{split} \begin{align*} t &= r\sqrt{\frac{n-2}{1-r^2}} \\ r &= \frac{t}{\sqrt{t^2 + (n-2)}} \end{align*} \end{split}\]
from scipy.stats import ttest_ind, pointbiserialr # or pearsonr

r_result = pointbiserialr(x_binary, y)
r = r_result.statistic

# Make groups using boolean indexing
group_a = y[x_binary == 0]
group_b = y[x_binary == 1]

t_result = ttest_ind(group_a, group_b)
t = t_result.statistic

#  r -> t
t_from_r = r * np.sqrt( (len(binary) - 2) / (1 - r**2))

# t -> r
r_from_t = t / np.sqrt(t**2 + (len(binary) - 2))

# True
t == t_from_r
r == r_from_t

Spearman (Rank) Correlation#

Definition: Transform data to ranks and then calculate Pearson correlation on the ranks

Intuition: Whereas a Pearson correlation assumes that both variables move at a constant rate with respect to each other (linear relationship), Spearman correlation only assumes that the order of both variables move together at a constant rate (monotonic relationship).

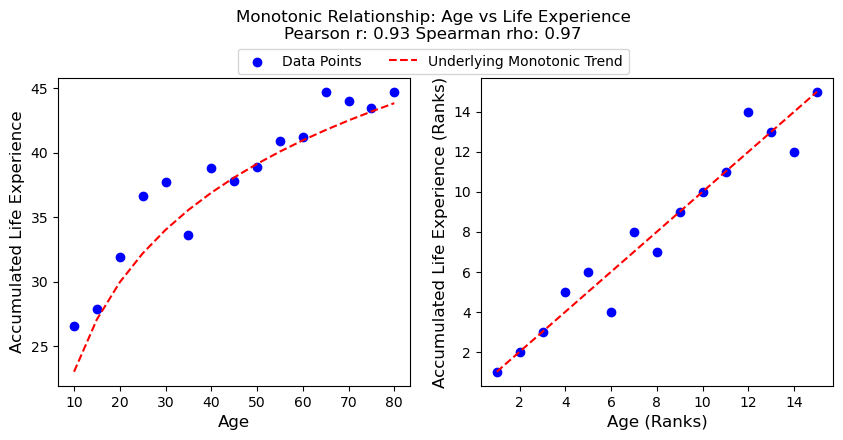
Figure 1

In other words, both variables must move together in the same direction (increasing or decreasing) but not necessarily at the same rate. For example, a person’s age and their accumulated life experience have a monotonic relationship. As a person gets older, their life experience tends to not only increase, but increase at a different rate than how age increases over their lifetime.

Rank-transforming them will normalize these different rates of change into units of “rank-change” - making Spearman correlation more sensitive than Pearson correlation in situations of skewed distributions or outliers.

# Rank the data
from scipy.stats import rankdata
x_ranks = rankdata(x)
y_ranks = rankdata(y)

# Compute Pearson correlation on ranked data
results = pearsonr(x_ranks, y_ranks)

# In practice just use spearmanr directly:
from scipy.stats import spearmanr

results = spearmanr(x, y)

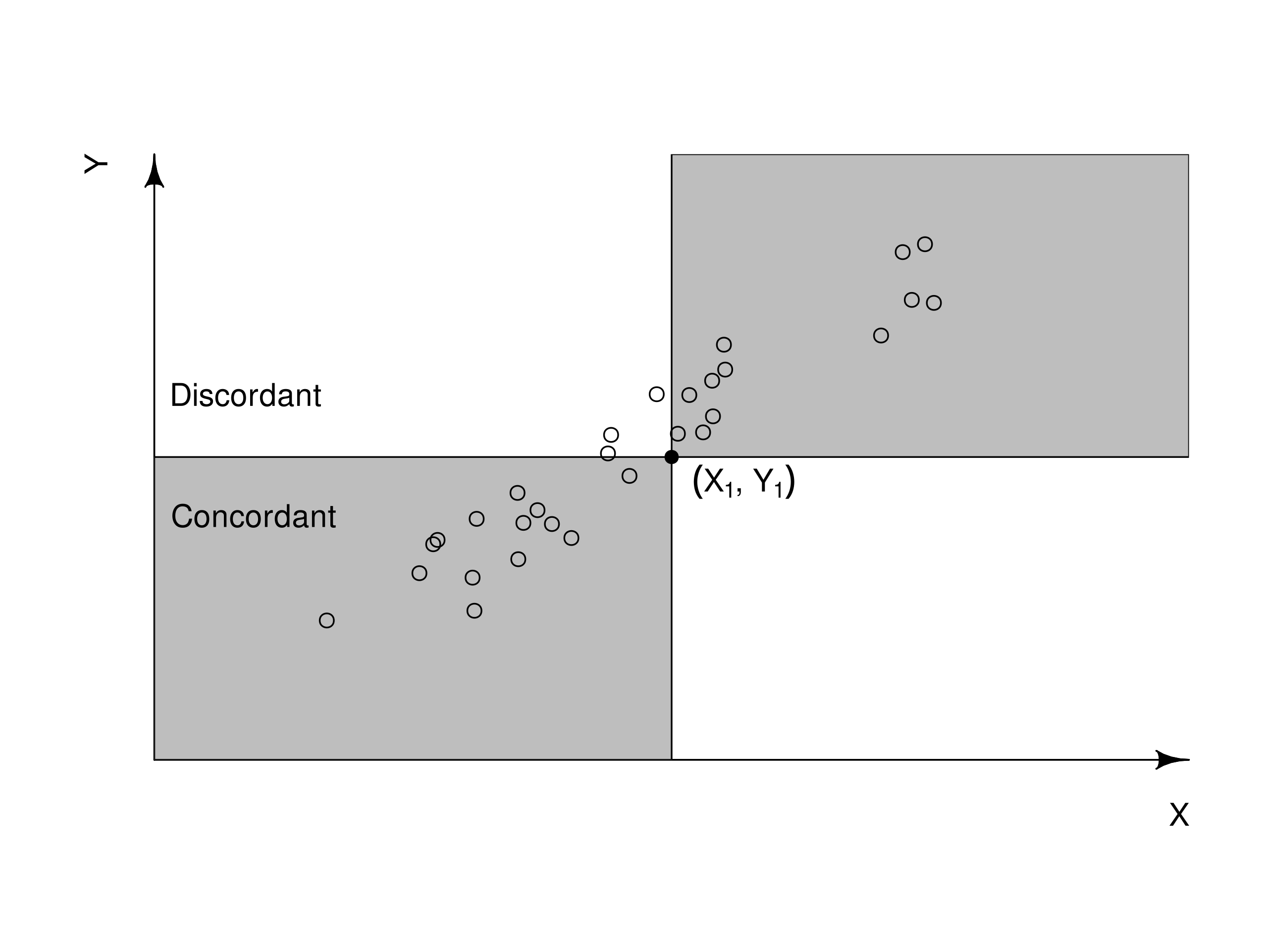
Kendall’s Tau (Rank)#

Definition: Count the proportion of \((x,y)\) pairs that are concordant vs discordant

Intuition: Also works with ranks and measures monotonicity by literally counting up pairs of \((x,y)\) that increase/decrease together (concordant) vs those that don’t (discordant). It’s particularly useful when dealing with small datasets or when rank-transforming produces lots of tied rankings.

Figure 1 
from scipy.stats import kendalltau

result = kendalltau(x, y)
Contents